Regular Expression(REX)

Basic concepts and properties

A language is regular if it is accepted by some FA(Finite Automata)

Regular Operations
- Union: $A \cup B = {w : w \in A o r w \in B}$
- Concatenation: $A \circ B = {a b : a \in A a n d b \in B}$
- Star: $A^{⋆} = {w_{1} w_{2} \dots w_{k} : w_{i} \in A a n d k \geq 0}$
The class of languages accepted by finite automata is closed under:
- Union
- Concatenation
- Star

Provement of Union

$\begin{aligned} \exists M_{1} = (K_{1}, Σ, δ_{1}, S_{1}, F_{1}) \\ \exists M_{2} = (K_{2}, Σ, δ_{2}, S_{2}, F_{2}) \\ c o n s t r u c t \exists M_{3} = (K_{3}, Σ, δ_{3}, S_{3}, F_{3}) \\ K_{3} = K 1 \times K_{2} \\ S_{3} = (S_{1}, S_{2}) \\ F_{3} = {(q_{1}, q_{2}) \in K_{1} \times K_{2} : q_{1} \in F_{1} \lor q_{2} \in F_{2}} \end{aligned}$

Provement of Concatentation

$\begin{aligned} M_{1} = (K_{1}, Σ, Δ_{1}, S_{1}, F_{1}) \\ M_{2} = (K_{2}, Σ, Δ_{2}, S_{2}, F_{2}) \\ M = (K, Σ, Δ, S, F) \\ l e t & K = K_{1} \cup K 2 \\ S = S_{1} \\ F = F_{2} \\ Δ = Δ_{1} \cup Δ_{2} \cup {q, e, s_{2} : q \in F_{1}} \end{aligned}$

Provement of Star

额外构造一个初始态，表示接受空串

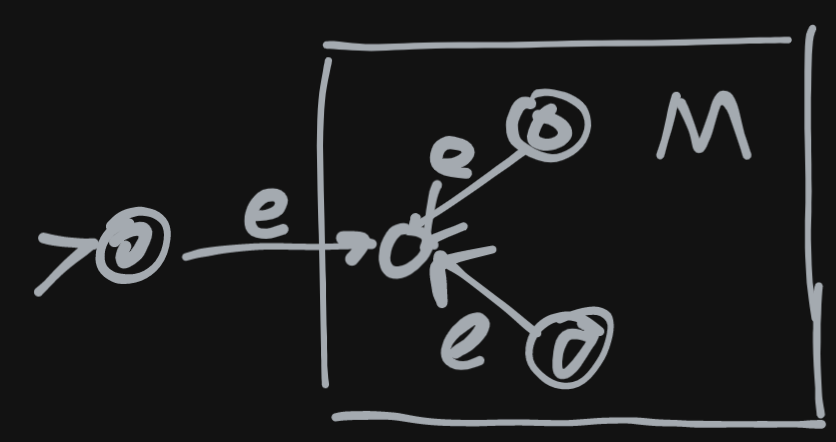
Atomic
- $\emptyset$ : $L (\emptyset) = \emptyset$
- $a \in Σ$ : $L (a) = {a}$
Composite ( $\cup, \circ, *$ )
- $R_{1} \cup R_{2}$ : $L (R_{1} \cup R_{2}) = L (R_{1}) \cup L (R_{2})$
- $R_{1} R_{2}$ : $L (R_{1} R_{2}) = L (R_{1}) \circ L (R_{2})$
- $R^{*}$ : $L (R^{*}) = (L (R))^{*}$
E.g.
- $L (e) = \emptyset^{*}$
- ${w \in {0, 1}^{*} : w h a s a t l e a s t t w o 0 s} = (0 \cup 1)^{*} 0 (0 \cup 1)^{*} 0 (0 \cup 1)^{*}$

Equivalence of REX and NFA

REX -> NFA
Operations of Union / Concatenation / Star can be easily represented by NFA.
NFA -> REX
- Let $L_{i j}^{k} = {w \in Σ^{*} : w d r i v e M f r o m q_{i} t o q_{j} w i t h n o i n t e r m e d i a t e s t a t e h a v i n g i n d e x \geq k}$
- Base case ( $k = 0$ )
  - if $i \neq j$ : $L_{i j}^{0} = {a : (q_{i}, a, q_{j}) \in Δ}$
  - if $i = j$ : $L_{i j}^{0} = {a : (q_{i}, a, q_{j}) \in Δ} \cup {e}$
- Goal: $L (M) = L_{(n - 1) n}^{n - 2}$ -> $R_{(n - 1) n}^{n - 2}$
- Recurrence:
  - $L_{i j}^{k} = L_{i j}^{k - 1} \cup L_{i k}^{k - 1} (L_{k k}^{k - 1})^{*} L_{k j}^{k - 1}$
  - $R_{i j}^{k} = R_{i j}^{k - 1} \cup R_{i k}^{k - 1} (R_{k k}^{k - 1})^{*} R_{k j}^{k - 1}$

Pumping Theorem

Let $L$ be a regular language. There exists an integer $p \geq 1$ , such that $w \in L$ with $| w | \geq p$ can be divided into 3 pieces $w = x y z$ , satisfying the followings:

for each $i \geq 0$ , $x y^{i} z \in L$
$| y | > 0$
$| x y | \leq p$

e.g. for $L = a b^{*} a$ , $p = 3$ .

The relationship between pumping theorem and regular

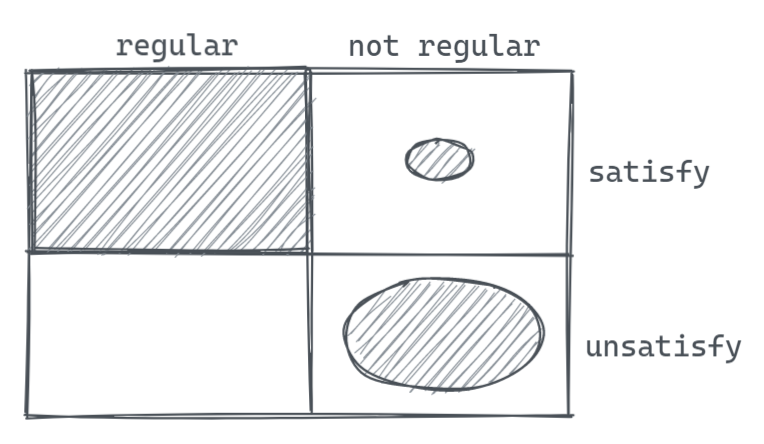
Example: Prove

0^{n} 1^{n}

is not regular.

Assume that $0^{n} 1^{n}$ is regular, let $p$ be the pumping length. Let $w = 0^{p} 1^{p} \in L$ , $w$ can be written as $w = x y z$ .
(1) $x y^{i} z \in L$ for any $i \geq 0$
(2) $| y | > 0$
(3) $| x y | \leq p$
(2)(3) -> $y = 0^{k} (k > 0)$ -> $x y^{0} z = 0^{p - k} 1^{p} \notin L$